基本概念
决策树:非参数,监督学习
xi的信息定义为
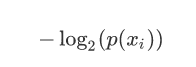
熵(Entropy):用信息的期望表示复杂度:
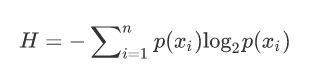
经验熵:概率用最大似然估计
信息增益(Information Gain):衡量复杂度的变化(base-new)
特征A对数据集D的信息增益
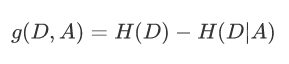
信息增益比:
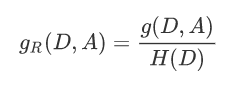
决策树的构造
选择特征对数据进行分割,递归分割,直到每个子集都被分到叶节点上去
停止分裂的条件:
(1)最小节点数
当节点的数据量小于一个指定的数量时,不继续分裂。两个原因:一是数据量较少时,再做分裂容易强化噪声数据的作用;二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
(2)熵或者基尼值小于阈值。
由上述可知,熵和基尼值的大小表示数据的复杂程度,当熵或者基尼值过小时,表示数据的纯度比较大,如果熵或者基尼值小于一定程度时,节点停止分裂。
(3)决策树的深度达到指定的条件
节点的深度可以理解为节点与决策树跟节点的距离,如根节点的子节点的深度为1,因为这些节点与跟节点的距离为1,子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度,当深度到达指定的上限大小时,停止分裂。
(4)所有特征已经使用完毕,不能继续进行分裂。
被动式停止分裂的条件,当已经没有可分的属性时,直接将当前节点设置为叶子节点。
常用算法:
ID3:离散型属性;选择特征时用信息增益作为标准;偏向选择取值较多的特征
ID4.5:离散、连续;信息增益比
CART:离散、连续;分类:基尼系数(Gini);回归:平方误差最小化准则;
参考资料: